Вероятность: основные понятия, структура, методы. - Скороход A.B.

3.1. Определение диффузионного процесса. Непрерывный
марковский процесс с вероятностью перехода P(s,x,t,A),
удовлетворяющей условию (33), называется диффузионным,
если для него выполнены следующие два условия:

I. Существует непрерывная функция a(t, х), определенная
на R+XRa со значениями в Rd, такая, что для всех е>0 и Т>0
равномерно по x£Rd и t^T

lim\ \ (у — х)Р(t, х, t-\-h, dy) =^a(t, x). (34)

\y—x\<e

II. Существует непрерывная функция B(t, x), определенная
на R+XRd со значениями в L(Rd), такая, что для всех е>0>
7>0 и и, zeRd

lim 4- [ (y — x,z)(y — x,v)P(t,x,t + h,dy) =

л—о п , J,

\у—х\<в

= (B(t, x)z, v). (35)

Векторная функция a(t,x) называется коэффициентом перено-
са диффузионного процесса, a(t,x) есть скорость течения в
среде, в которой находится диффундирующая частица. Опера-
торная функция B(t,x) называется оператором диффузии, он
характеризует дисперсию отклонения частицы от начального
положения, B(t,x)—неотрицательный симметричный опера-
тор, a(t,x) и B(t, х) называются диффузионными коэффициен-
тами процесса, точнее, если выбран некоторый базис в Rd
{е\,. .. ,ed), то диффузионными коэффициентами являются ко-
ординаты вектора a(t,x) в этом базисе: ah(t, х) = (a(t, х), ея)>
k = \,...,d и элементы матрицы оператора B(t, х) в этом ба-
зисе:

bih(t, х) = (B(t, х)е{, eh), i,k^d.

Простейшим примером диффузионного процесса в Rd является
винеровский процесс. Это однородный процесс с независимы-
ми приращениями %(t), для которого %,{t-\-h)—%{t) имеет нор-
мальное распределение со средним 0 и единичной корреляцион-
ной матрицей, т. е. распределение \(t-\-h)—\(t) имеет плот-
ность

Вероятность перехода для такого процесса задается равенством
P(s,x,t, A) = (2^(t-s))-"l^exp\-fIi~(y-x, y-x)}dy.

а

Простой подсчет показывает, что для всех т > О

\\y~x\mP{s, х, t, dy) = 0((t-s)mi2),
J (y — x)P(s, x, t, dy) = 0,

j (y — x, z) (y — x,v)P(s, x, t, dy) = (z, v) (t — s).

Поэтому £(/) является диффузионным процессом, для которо-
го а = 0, B = I, I— единичная матрица.

3.2. Уравнения Колмогорова. Наша цель — получить диф-
ференциальные уравнения, с помощью которых можно опреде-
лить вероятность перехода. Эти уравнения похожи на уравне-
ния диффузии, получаемые в физике, лишнее свидетельство
того, что название «диффузионный процесс» отражает существен-
ное в процессе. Предварительно установим одно вспомогатель-
ное предложение.

Лемма 1. Если ц>(х)—числовая функция на Rd, ограни-
ченная и непрерывная, дважды дифференцируемая в окрест-
ности некоторой ТОЧКИ Xq, то

Urn4" ГС (p(y)P(t, х0, t + h, dy)-y(x0) =

= {a(t, х0), <V(x0)) + ±SPB(t, x0)y"(x0) (36)

(Ф" (xQ) — оператор_из L(Rd), для которого

(Ф" (х0) и, v) = ф (х0 + tu+ sv) J<=o,

Sp А— след оператора А).

Доказательство. Имеем для всякого е>0

§(Ф0/) — Ч(х0))Р (t, х0, t + h, dy) =
j (Ф(У) — ФЫ) P(t, х0, t + h, dy) + o(h) =

j (Ф' {x0), у - jc0) P(t,x0,t + h, dy)+

\х—у\<г

+ jj 4(ф,/ (хо)(У — хо)> y~x0)P(t, xQ, t + h, dy) +

\х—у\<г

\х—у\<г

+1

ае I у — х(

\2Ру, х0, *+А, йу) + о(Н),

где

а, \ у — х0 |2 = Ф(у) — фрс0) —
- (ф' {х0), У — х0)—2~(ф" (х0) (у — х0), у - х0).

аЕ-*0 при е->0. Воспользовавшись соотношениями (34) и (35),
получаем (36). □

Теорема 1. Пусть фбСд^ и функция

дважды дифференцируема по х, производные и'х и и"х непрерывны
по 5. Тогда при s<t она удовлетворяет следующему дифферен-
циальному уравнению

Доказательство. Имеем на основании леммЫ

и (5—А, х) — и(8, Х) = \и(3, у) Р(5—А, X, 5, йу) — и($, х) =

Отсюда вытекает, что и (я, х) имеет левую производную по 5,
ее значение равно левой части (37), взятой с минусом. Значит,
она непрерывна и поэтому совпадает с обычной производ-
ной. □

Можно уравнение (37) связать с диффузионным процессом
еще и так.

Теорема 2. Пусть функция и(5, х) при непрерывна и

ограничена и имеет непрерывные ограниченные производные
г^(5, х), и'х(8, х), и'хх(з, х). Если для и(5, х) выполнено уравне-
ние (37), то

Доказательство. Для доказательства формулы (38)
достаточно показать, что и (я, %($)) является мартингалом.
Имеем

М(Я(5 + А, |(5 + А))||(5))=$Р(5, |(5), 5+А, й?у)й(5+А, У) =

= й (5, !(«)) + «; (я, |(5))А + о(А) + 5й(5, «/)/>(*,£(«). « +А, =

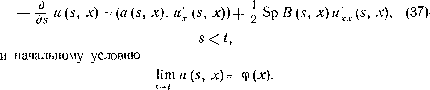
(38)